Supplementary videos from "Force and Flow Transition in Plowed
Granular Media"
Nick Gravish1, Paul B. Umbanhowar2, Daniel I. Goldman1
1School of Physics, Georgia Institute of Technology, 2Dept. of Mechanical Engineering, Northwestern University
 |
 |
In these experiments we dragged a flat plate through granular media (250 micron diameter glass beads) and observed how the drag force and granular flow changed as a function of prepared volume fraction. At the loosest packing (volume fraction=0.579) we observe small fluctuations in the drag force and a smooth advance of the flow field with the advancing plate.
Repeating the experiment with the plate aligned next to a clear wall allows for visualization of the granular flow. In the loose packing (with colored beads added on the top layer) the grains deform smoothly with no localized regions of flow.
In the densest packing (volume fraction=0.620), when the material is packed above the measured dilation transition (at volume fraction=0.603), we observe sharp intermittent upwellings of material that are periodic and bounded by an interface which separates the flowing and stationary grains. <\p>
The periodic formation of these localized flow boundaries is clearly observed when viewed in the side view experiment. As the plate advances shear planes are periodically formed which separate the stationary and flowing regions.
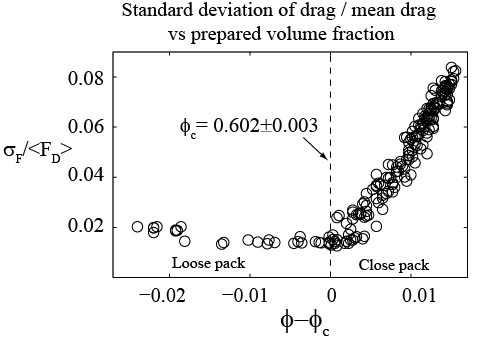
Signatures of the formation of these shear planes during drag are observed in the drag force as periodic large amplitude fluctuations, and so by measuring the drag force fluctuations (std. deviation of drag) we observe that the onset of the shear localization coincides with the measured onset of dilatancy in the granular media (below).
Using the particle image velocimetry (PIV) technique we extracted out the velocity field of the granular flow from the side view experiments (velocity magnitude shown below at bottom). We measure the shear plane angle (θ) and observe that in the closely packed media, the shear is highly localized and the evolution of θ is correlated with the evolution of the drag force (right).
We construct a model of the shear plane evolution in the close pack considering that the drag force on the plate is in equilibrium with the gravitational and frictional forces exerted on a flowing wedge at variable angle θ. The shear plane once initiated is pinned to the top surface and bottom of the plate (below a) and so θ increases with plate displacement. Assuming the coefficient of friction along the shear plane increases with prepared volume fraction, we find that as θ increases the drag force required to maintain equilibrium increases until eventually the plate is pushing with enough force to initiate the failure of a new shear plane at shallower angle θmin , at this point the cycle repeats (below b).

Comparing the model dynamics and the observed experimental dynamics at close pack (below) shows good agreement between the predicted and observed evolution in FD vs θ space.