Jeffrey Aguilar || Alex Lesov || Kurt Wiesenfeld || Daniel I. Goldman
CRAB Lab @ Georgia Institute of Technology
Publication:
Lift-off dynamics in a simple jumping robot
We study vertical jumping in a simple robot comprising an actuated mass-spring arrangement. The motor is given a sine wave, and frequency and phase are systematically varied to find optimal performance by measuring jump height. One might expect the best jumps to occur at resonance. But that is surprisingly not the case. Optimal jumps occur above and below (but not at) the robot’s resonant frequency, f0.
Low Power
Stutter Jump:
High Power
Single Jump:
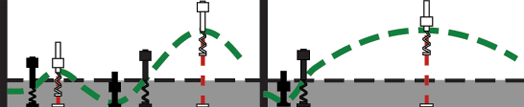
Two distinct jumping modes emerge, both with similar jump heights: The single jump which is optimal above f0 and is achievable with a squat maneuver, and the lower power stutter jump which is optimal below f0 is generated with a counter-movement.
The single jump may be faster, but requires much more power to produce. A tradeoff between power and time-to-lift-off must be made.
Built with Processing.js

Animals and robots must run, crawl, and jump over a diversity of substrates through effective motion of their appendages. Jumping is particularly interesting, since it involves a transient burst of activity. It is essential to many animals and robots that must regularly reach higher ground, escape predators, or simply use jumping as a primary means of locomotion.
Biological studies have revealed mechanisms of jumping in many organisms. In robotics, biologically inspired legged jumping robots have been constructed as an alternative to wheeled robots to better traverse rough terrain. The initial movement strategies for optimal jumping are typically chosen by empirical tuning for steady state hopping or squat jumps. But what types of jumps provide optimal performance? How is this affected by mass, size, and body stiffness? Systematic studies to answer these questions from the perspective of the transient dynamics of jumping are relatively scarce.
Choosing a theoretical jumping model for such a study that can allow us to ask and more importantly, answer, these questions is essential. While both simple and complex models have been created to study optimal movement patterns, simple models can be fully analyzed and provide guidance for simplifying control of more complex devices, and even reveal principles of biological locomotion. As such, in our study, we choose a simple 1-D mass-spring system with an actuated mass.
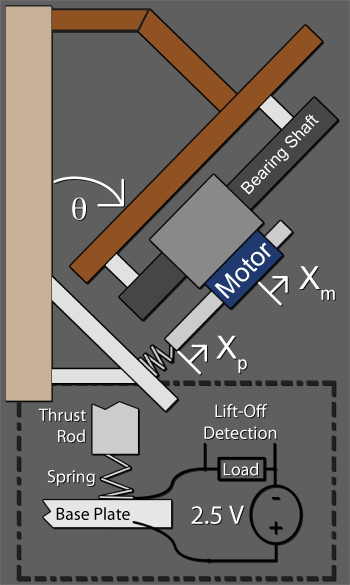
A linear motor was attached to an air bearing for near frictionless 1D motion. Due to the weight of the air carriage, the apparatus was slanted to an angle of θ = 75° to reduce the gravity load on the motor to 0.276g.
Total mass load on spring: m = 1.178 kg
Spring stiffness: k = 5.8 kN/m
Damping ratio: ζ ~ 0.01 (from video tracking data of free oscillations)
Lift-off was detected at a rate of 1000 Hz by reading the voltage of a circuit that would open and close at the interface of the bottom of the spring and the metal base.
Procedure:
1. Robot in equilibrium at rest
2. Move motor position (Xm) as a sine wave for 1 cycle with 4 mm amplitude at a given phase (Φ) and frequency (f).
3. Calculate jump height from air time.
4. Repeat 3 times for each of 6720 different combinations of (Φ,f).
A concurrent simulation reproduced the experiment by integrating the following equation of motion:
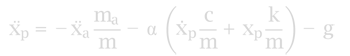
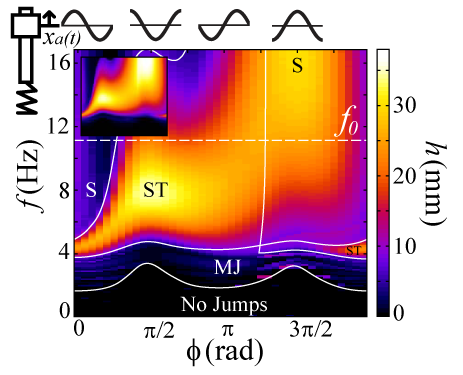
The the results of 6720 combinations of (Φ,f) each averaged over 3 trials are shown here in the (Φ,f) plane. These results were verified with simulation (top left inset). There are two general peaks in height in the stutter jump (ST) region and the single jump (S). These regions were found using simulation, where MJ is an area of low jump height multi-jumps.

Two peaks in jump height occur at a phase of π/2 and 3π/2. The π/2 (countermovement) jump is a stutter jump that occurs at a slower frequency than f0, so, combined with the fact that there is an intermediate hop, it results in slower take-off. At 3π/2, a faster single squat jump occurs, which also requires more internal deformation power.
Comparing with Kobe